半導体産業における「風を読む」IV〜2011年のシリコンウェーハ出荷面積の動向

また、2011年1月IMF、World Bank においてGDPの改訂版を公表したことから、前回値と今回改訂値との比較、さらにあまり知られていないが、公的機関である国連貿易開発会議(United Nations Conference on Trade and Development：UNCTAD)より2011年1月、GDP数値が公表されたので併せて紹介する。

表1は、GDPについて第二回目で紹介したIMF、World Bankによる前回GDP（成長率）公表値と今回の公表に伴う改訂値、および下記に紹介する数式Inoue Formulaで使用する当年GDP変換値（当年GDP-前年GDP）の前回値と今回の公表に伴う改訂値、UNCTADのGDP予測値を示す。

表1　公的機関によるGDP公表値と具体的なGDP数値の変換例（2009〜2012年）　比較

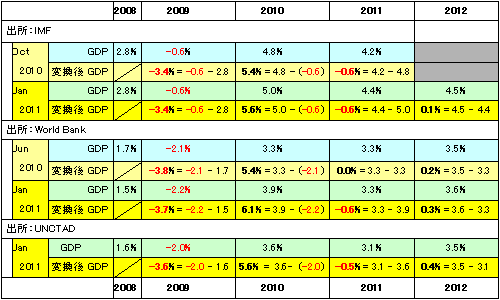
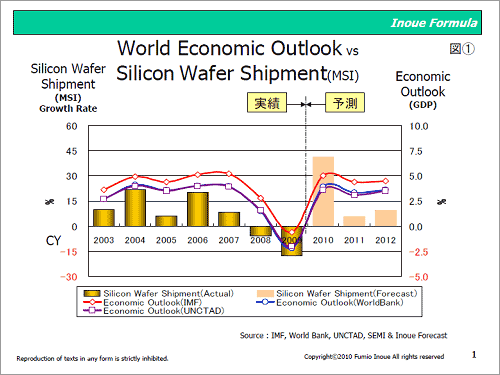
図1　GDP（成長率）とシリコンウェーハ出荷面積（成長率）との動向比較

図1は、IMF、World BankおよびUNCTADが公表している全世界ベースでのGDP（成長率）とSEMIが公表しているシリコンウェーハ出荷面積のデータにより算出した成長率（前年比）を2003〜2012年の10年間に渡り図示化したものである。本図より三つの公的機関によるGDPとシリコンウェーハ出荷面積との間において連動性がある様子を理解できる。

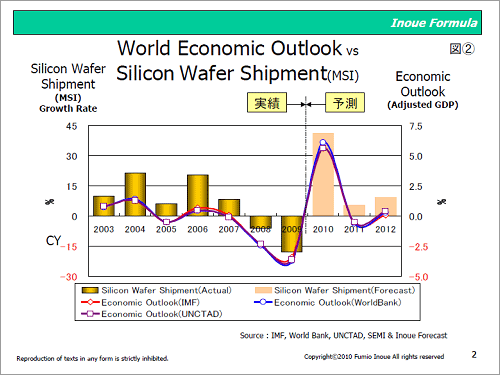
図2　変換したGDPとシリコンウェーハ出荷面積との動向比較

図2は、GDPについて表1に示す「当年GDP変換値=当年GDP-前年GDP」と、GDP数値を変換した後、図1と同じ内容を図示化したものである。この図から、GDPを数値変換することにより、GDPとシリコンウェーハ出荷面積との間でより一層連動性を持ちながら変化している様子を理解できる。

また、表1、図2より理解できる点としてGDP変換値は、IMF、World Bank及びUNCTADがほぼ同一となることである。 即ち、IMF、World Bank にUNCTADを加えた三つの公的機関は、一見異なるGDP予測数値を公表しているように見えるが、第二回目で説明している設備投資、消費活動への原動力を示すGDP変換値がほぼ同一であることから、経済に対する影響力と言う見方をすれば、同じ内容（原動力）を公表していると言える。

これらの数値が半導体産業の市場を予測する上で非常に有益なのは、予測の数値があまり変動せず、市場の先行きの考え方を大きく変更しなくて済むことである。これまで、半導体関連市場は先が見えにくいと言われてきた。IMF、World Bank、UNCTADという三つの公的機関の予測は、多少の変動があっても内容（風の向きや強さ）そのものがほとんど変わらない。このため、一年先の市場観に対する考え方を変えずに済む。このことはビジネスを行う上で極めて有益である。

シリコンウェーハ出荷面積の1〜2年先の成長率（前年比）に対する予測値のガイドラインは、下記の数式Inoue Formulaで知ることが出来る。具体例として、IMFの最新データである2011年1月版を使用すると、2011年のシリコンウェーハ出荷面積の成長率ガイドラインは次式のようになる。

Inoue Formula 　2011年　= α x ( -0.6%〔変換後GDP〕　+ β) =2.4%　　---　数式A

定数α、βに対する論理的な算出は現状できていないが、経験則として「α=6, β=1.0%」を採用する。

第二回目で半導体市場、第三回目で半導体製造装置に対し紹介したように、公的機関が公表するGDP（成長率）を使用することにより、1〜2年先における半導体市場と製造装置市場の変化（風の流れの方向と強さ）を数式で示すことが可能である。同様に、シリコンウェーハに関しても数式にて示すことができるのである。　

表2は上記の数式Aを使用し、2009〜2012年の4年間に渡り、シリコンウェーハ出荷面積に対する成長率のガイドラインを示したものである。IMFとWorld Bankについては、前回と今回改訂公表値を用い、UNCTADについては今回の公表値を使用して算出した。

表2：　Inoue Formulaによる　シリコンウェーハ出荷面積　成長率（前年比）ガイドライン

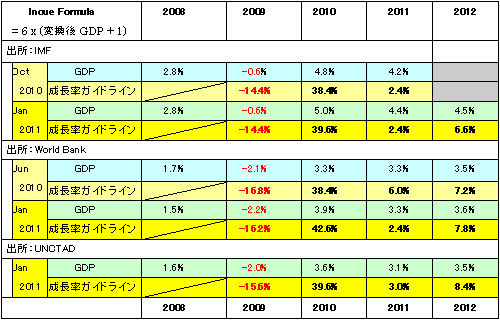
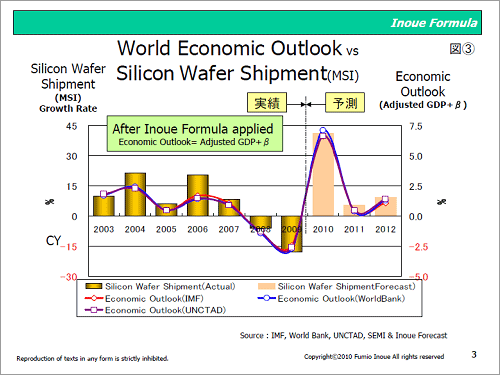
図3　Inoue Formula（数式A）にてパラメータ変換したGDPとシリコンウェーハ出荷面積との動向比較

図3は、表1に示すGDP変換値に定数βに加えたInoue Formulaにて算出した数値(表2)とシリコンウェーハ出荷面積の成長率（前年比）を図示化したものである。この図より、経済指標であるGDPとシリコンウェーハ出荷面積があるパラメータを介することにより、GDPとシリコンウェーハ出荷面積との間における相関関係において、より一層緊密に連動していることを理解できる。

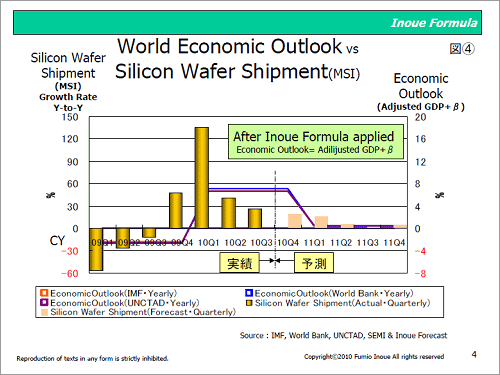
図4　四半期ベースでのシリコンウェーハ出荷面積とInoue Formula（年間ベース）との成長率比較

表2に示すInoue Formula（数式A）にて算出したシリコンウェーハ出荷面積の成長率ガイドラインは、暦年ベースの平均値である。図4に示すように四半期ベースで前年同期比を見た場合、2010年のような年間平均成長率が高い場合にはピークとボトムで大きな差があり、同じ年であっても異なる市場観を生み出す。しかし、2011年のように年間平均成長率が低いと想定される場合には実質上、年間平均成長率と四半期ベースでの成長率との差がなく、同じ市場観を持つことができると考える。
　
半導体市場の成長率のガイドラインについては、第二回目で紹介したようにIMFの最新データである2011年1月版を使用すると、2011年の半導体市場の成長率ガイドラインは次式となる。

Inoue Formula 　2011年　= α x (–0.6%〔変換後GDP〕　+ β) = 7.0%　---　数式B

定数α、βについては、第二回目で説明している「α=5, β=2.0%」を採用する。

半導体市場とシリコンウェーハ出荷面積との連動性は、上記数式AとBから変換後GDPを介し、数式を求めると次式Cとなる。

シリコンウェーハ出荷面積の成長率　=　1.2　x（半導体市場の成長率　– 5.0 % ）　　---　数式C

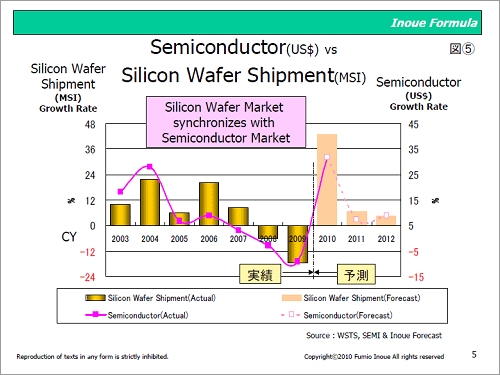
図5　Inoue Formula(数式C)においてパラメータ変換した半導体市場とシリコンウェーハ出荷面積との年間ベースでの動向比較

図5は上記数式Cをより一層理解してもらうため、半導体市場とシリコンウェーハ出荷面積の成長率を数式Cのパラメータを介し図示化した。相関関係を持ちながら連動している様子を理解することができる。

なお、上記数式A、B、Cは一次方程式であるが、計算を容易にするためであり、より一層高い近似性を求めるのであれば、二次元方程式、三次元方程式と、より多次元化することにより数学的には可能である。

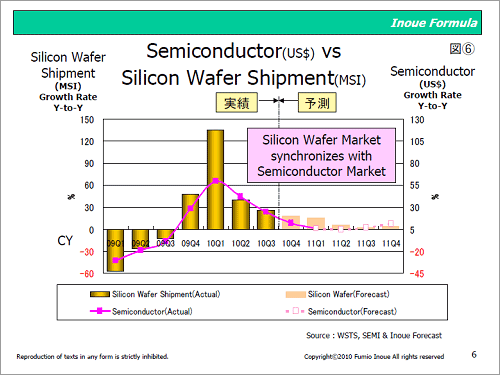
図6　Inoue Formula(数式C)においてパラメータ変換した半導体市場とシリコンウェーハ出荷面積との四半期ベースでの動向比較

図6は、図5と同じ内容を2009〜2011年の3年間に渡り12四半期を図示化したものである。本図より数式Cが四半期ベースの動向比較に対しても適応可能と考えられる。

シリコンウェーハ市場に関する公的なデータとしては　SEMIとは別にSICAS(Semiconductor International Capacity Statistics-世界半導体生産キャパシティ)が四半期ベースで　そのﾃﾞｰﾀを公表しているが、このSICASに対する半導体産業における数学的相関関係は次回、紹介する。

参考資料：
1. 国際通貨基金(International Monetary Fund-IMF) ホームページ
2. 世界銀行(World Bank)ホームページ
3. 国連貿易開発会議(United Nations Conference on Trade and Development-UNCTAD)ホームページ
4. 世界半導体市場統計(World Semiconductor Trade Statistics-WSTS) ホームページ
5. 国際半導体製造装置材料協会(Semiconductor Equipment and Materials International: SEMI) ホームページ
6. 半導体産業における「風を読む」III〜半導体製造装置市場動向
7. 半導体産業における「風を読む」II〜GDPと半導体市場との相関関係から導く
8. 半導体産業における「風を読む」I