����ǽ�ؤ�ƻ��7�ˡ���ΨŪ�������о�а�
��ΨŪ������ɽ����ˡ
�ֿ���ǽ�μ¸��ˤϡس���Ū�������٤�س�ΨŪ�������٤˳�ĥ����ɬ�פ�����פȡ����ƻ�Ŧ�����Τϡ�1986ǯ����ʸ��Probabilistic Logic�ˤ�ȯɽ�����˥륹���ͥ륽����Nils J. Nilsson������������ե�������ؤΥ���ԥ塼���������ζ����ˤ��ä��Ȥ����Ƥ��롣�ʻ��ͻ���1�ˡ�
1986ǯ�Ȥ����ȡ�100���ǻҤ�Ķ������åפ��̻�����Ϥ����Ǥ��롣 �緿����ԥ塼���Υ����������Ϥޤꡢ�͡��ʽ��Ѳ�ϩ�߷��Ѥ�EDA�ġ���Υ��եȥ������������졢ICOT�ʿ����女��ԥ塼�����ѳ�ȯ�����ˤˤ�륨�����ѡ��ȥ����ƥ೫ȯ�����ú�����ä�����Ǥ⤢�ä���
�ֳ�ΨŪ��������ɬ�ספȤΥ˥륹���ͥ륽���μ�ĥ�������Υǥ��������̿���������ˤƤɤΤ褦�˰���줿�Τ�ɮ�Ԥ�Ĵ���ڤ�Ƥ��ʤ��� �������ʤ��顢����Ū�ʥޥ�����߷פˤϡ���ΨŪ���������Ѥ�����Ϥ����פȤθ���ϡ����Ѳ�ϩ��ȯ���Ϥޤ������ʳ��Ǥϡ��ष�������̤��ä��ΤǤϤʤ�������������
�㤨�С���˾�����ŻҲ�ϩ���Ѥ�������ԥ塼���γ�ȯ��Ԥä��ե��Υ��ޥ��ϡ�1952ǯ�˥���ե���˥�������ؤǹԤä��ֱ��"Probabilistic Logics and the Synthesis of Reliable Organisms from Unreliable Components"�����ͻ���2�ˤ�ʤ��ˤ����äơ����ܲ�ϩ���ΨŪ������ǥ�ʿ�1�ˤȤ��Ƥ����� ���δ���������ϩ��ǥ�ϡ�1943ǯ�Υޥ����å�&�ԥåġ�MacCulloch&Pitts�ˤο��˥塼�����ǥ�Ǥ��ä��ʻ��ͻ���3��4�ˡ�
ȾƳ�ν��Ѳ�ϩ������������������ʳ��Ǥϡ��ʤ�����ǽ��������ˤϳ�ΨŪ������ɽ������黻�Ҥ�ɬ�פȸ��Ƥ����Τ���������
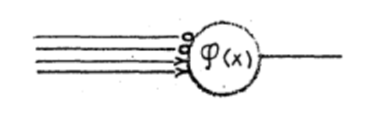
��1���ե��Υ��ޥ�1952ǯ�ιֱ�Ǽ����������ȥޥ� (Automata) ��������뤿������ʤδ��ܥ�ǥ롡���Υ�ǥ���ܴﴱ (Basic organ) ���⤷���ϡ�ñ���ϥ����ȥޥȥ� (Automaton) �ȸƤ�Ǥ����ʻ��ͻ���2�ˡ� ���Υ�ǥ�ϡ�1943ǯ�����줿�Ȥ���Ƥ���ޥ����å�&�ԥåġ�MacCulloch&Pitts�ˤο��˥塼����ʤ⤷���ϡ������˥塼����ˤΥ�ǥ�ȴ���Ū�ˤ�Ʊ���Ǥ���ʻ��ͻ���3��4�ˡ�
��ŵ��Automata Studies, Princeton University Press�ʻ��ͻ���2��
�ޥ����å�&�ԥåĤο��˥塼�����ǥ�ϡ��˥塼����ν��Ϥ��������ˡ��ޤ������ʥץ����νŤߤ�ɽ���٥��ȥ�{ wi }�ȡ����Ͽ��椬ɽ���٥��ȥ�{ xi }�������ͤ�������1�ˡ� �����ͤϡ��٥��ȥ�{ wi }�ȥ٥��ȥ�{ xi }�θ�����Ʊ���Ǥ�����˺���Ȥʤ�Τǡ�ξ�٥��ȥ�֤Ρָ����פΰ��פ����٤�ɽ�����٤Ȥʤ롣�⤷���٥��ȥ��Ĺ�������ʲ�����Ƥ���Ȥ���ȡ������ͤϡ��٥��ȥ�ν����֤Ρֵ�Υ�פǤ⤢�롣
ɮ�Ԥϡ����˥塼������Ĥξ���ʳؽ��ˤ�äƳ��������٥��ȥ�����ϥ٥��ȥ�ˤΡִ������ספǤϤʤ���ξ�٥��ȥ�Ρָ����ΰ��פ����١פ�ֵ�Υ�ζᤵ�פ��Ѥ��������黻��ԤäƤ��뤳�ȼ��Τ����ֳ�ΨŪ�����פν��������ĥ�����Τ��Ȼפ��� �ָ����ΰ��פ����١פ�ֵ�Υ�ζᤵ�פϡ��Գ��ꤵ����Ƥ���Ω���������� ��������Ƥ��ƿʤ�������ϡ����ˡֳ�ΨŪ�����פǤ��롣
�����ǡ��ʲ��ˡ��ֿ��˥塼�����ư�����ΨŪ������Ÿ���Ǥ���פȸ�������ͳ��ϩ���Ѥ����ǻҤ修��δ�������ȡ���ϩ���������������̤���ޤȤ�Ƥߤ���
�ǻҤ修��δ������鸫��ֳ�ΨŪ������
���˥塼����ǥ벽���褦�Ȥ�����к�˦��ȯ��ư������⤽���ΨŪ���ä����Ȥ�פ��Ф��Ƥ������������� �ºݤο��к�˦�ˤ������ȯ�и��ݡפϡ��ֿ��к�˦���æʬ�ˤˤƾ徺�������Ṳ̋����Ͱʾ�Ȥʤä����˵���ʿ�2�ˡפȤ���Ƥ����������������Ṳ̋ϡ����ꤷ�������Ṳ̋ǤϤʤ��ä�����2�ˡ�
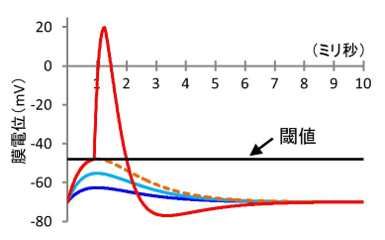
��2�����к�˦�κ�˦��γ�ư�Ű̡�Action Potential�ˤ����ͤδط�����˦���ή������������ˤ�����Ṳ̋�ʬ�ˤ������͡פ�ۤ���ȡ���æʬ�ˡפȤ����ݥ��ƥ��֥ե����ɥХå����ݤ������ꡢ�ѥ륹���γ�ư�Ű̡��֡ˤ�ȯ������פȤ��롣����ŵ��Web���Ǿ�ʳؼ�ŵ��2012ǯ4��3���ǡ�
�ֺ�˦���ξ�̤��Ű̺������Ű̡ˤ����ͤ�Ķ����ȡ��ݥ��ƥ��֥ե����ɥХå��������ԡˤ������ꡢ�����Ṳ̋���˾徺����פȤ������к�˦��ȯ��ư��ϡ�ȾƳ�Υȥ������Ȥä���ư��ϩ��ư��Ȼ��롣 ��ư��ϩ��ư����Ͷ�˵�Ǥϳ�ΨŪ�ˤʤ�ʾ塢���к�˦��ȯ�Ф��롿���ʤ���Ƚ������Ͷ�˵�Ǥϳ�ΨŪ�Ȥʤ�Τ��ԻĤǤϤʤ������ͻ���5�ˡ�
�����⡢���к�˦�����Ͽ���ο��濶����100mV���٤����ʤ��������̣�Ǥϡ����к�˦�ؤ����Ͽ���ϡ�������Ͷ�˵��ɺ�äƤ���Ȥ�����롣 �ºݤο��к�˦�Ǥϡ����ޡ��������ȯ�и��ݡʼ�Χȯ�Сˤ������뤬������ϡ�ȾƳ���߷פ�и������ʹ֤Ǥ���С������ϥ�٥�����ͤΥ��졼������������ꤷ�Ƥ���Τ����顢��ư��⤢��������פȸ��äƤ��ޤ������ʸ��ݤǤ���ʻ��ͻ���6�ˡ�
�ޥ����å�&�ԥåĤο��˥塼����⡢�ե��Υ��ޥ���ñ���ϥ����ȥޥȥ�⡢���к�˦��ư�����ľ�ˤ��Τޤޥ�ǥ벽�������ᡢ���ܲ�ϩ��ǥ��ư����ΨŪ�Ȥ����ȤϹͤ����롣 ���в�ϩ������Ÿ������ľ�˴ѻ�����ȡ�����ϡ��֥Υ���ȯ����ȼ����Ψ�����פȸ�����Τ�������
���к�˦�������������Ͼ�������Ͽ��淲�ˤ��礭�����ֳ�ΨŪ�����פ�ɬ�פ���
���к�˦�ؤο������Ϥ��ܿ�������¿���������פ��Ť餤���ᡢ�֤ۤܰ��פ������֡פ��Ѥ���������ʤ������ͭ�Ѥ��ä��Ȥ�����ΤǤϤʤ�����������
���⤽�⡢���˥塼����⡢���¤ο��к�˦�⡢���̤ˡ����ʥץ����θĿ�������¿���� ¿�����ˤϡ�1000��ͥ��Ķ���륷�ʥץ������ˤ�äơ����ʥ˥塼����ο��������Ƥ��롣 �Ĥޤꡢ���Ͼ�����ϼ�������٥��ȥ�{ xi }�ȳؽ��ˤ�����������������������ϼ�������٥��ȥ�{ wi }�μ������϶��������礭���� ���äơ�ξ�٥��ȥ뤬����Ʊ�������������ǽ���������㤤�Ȥ����롣 ʸ�ϡ����ڡ����衢�������οʹ֤��оݤȤ������⡢���٤�Ʊ��ɽ���˽в��Ȥ�̵���Ȼפ�������ʣ���ξ����פ����Ψ���㤤��Τ���
���ʿ��������ˤơ������=�ˤ���̣����ָ��ʤʰ��ספ����פǤ��ꡢ���������Ǥ������=�ˤν������������Ȥ��Ƥ⡢���������ʹ֤�Ǿ���Ԥ��ǡ��������ˤ����Ƥϡ������=�ˤ���Ω���뤳�ȤϤۤȤ�ɤʤ��ΤǤ��롣 ���ΰ�̣�ǡ�ʸ�ϡ����ڡ����衢���ʡ����ξ�������ˤ����Ƥϡ������=�ˤν����٤��㤤�Ȥ⤤���롣 ���������ξ���ϡ��оݤ�ѻ������Ѳ����Ƥ���Τ��̾�Ǥ��ꡢ���ˡ�����ˤϥΥ�����ޤޤ�롣 ����Ū�ˤϡ�����ʢ�ˤˤơ����֤�Ƚ�̤��ơ�������Ÿ�����뤷���ʤ��Ȥ�����롣
�Ȥ������Ȥϡ������=��ư����濴���Ȥ�Ω�Ƥ�줿���ߤΥ����å����Ѳ�ϩ�ϡ�����ʢ�ˤ��濴�Ȥʤ�ʸ�ϡ����ڡ����衢���ʡ����ι��٤ʾ�������ˤϸ����Ƥ��ʤ��Ȥ������Ȥˤʤ�ʤ�����
�����å����Ѳ�ϩ�ϡ����̤ˡ���3�Τ褦�ʿ�����ɽ��ư����Ѥ����߷פ���롣�����Ū�����ܿ��ξ��ʤ�AND��NOR�ʤɤδ��ܲ�ϩ�Ǥ��롣���ܲ�ϩ�ϡ�������ɽ�����ϡ�X1�ˤ����ϡ�X2�ˤ��Ȥ߹�碌���������ס�=�ˤ����ԤΡֽ��ϡ�Y�ˤ�����͡פ���Ϥ��롣
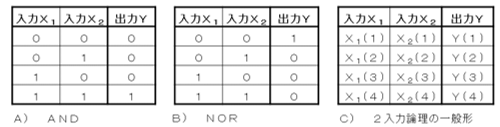
��3������ԥ塼���ǻȤ�����ܱ黻��ϩ�ο�����ɽ���㡡2���Ϥο�����ɽ�ΰ��̷��ϡ�C�ˤΤ褦�ˤʤ뤬����ΨŪ�����ξ��ϡ��ƿ��ͤ���Ψ�ͤȤʤꤦ�롣����ŵ��ɮ�Ժ���
����������������¿��������ν����˺�Ŭ�����줿���˥塼����ʷ��ˤο�����ɽ�ϡ���4�Τ褦�����������ܿ����礭��ɽ�Ȥʤ�������� ���ˡ��ƹԤν��Ϥ�����ͤ�0��1�δ֤��ͤ����Ψ�͡פȤ��ơ�����1�����Ϥ�����Ψ�פ��Τ����Ѿ�ͭ�ѤȤʤ롣
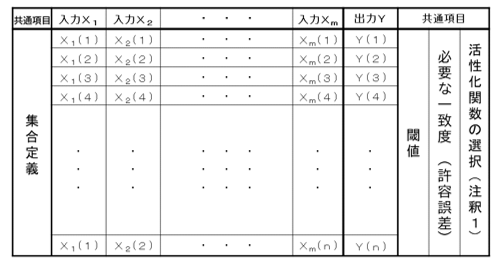
��4���˥塼�����ǥ��ɽ�����뿿����ɽ���㡡����¿���ϤǤ��ꡢ���Ϥ���Ϥ�����ͤˡֳ�Ψ�͡פ��о줹��褦����ɽ�Τ褦��ɽ�Ȥʤ롣 ��ΨŪ�����ˤϡ��طʤȤ��ơ��ֲ��ν���ˤƳ�Ψ������ˤ��뤫�פ䡢�֥���ץ���ʹ�סˡפ����Τˤ������ˡ��ֶ���ʢ�ˤ�����Ω�Ĥȸ��������Ρ�ɬ�פʰ����١١��⤷���ϡ��ص��Ƹ����١��������β�����ɬ�פ����뤿�ᡢ���Τ褦�ʹ��ܤܤ�������ɲä��Ƥ��롣�ʤ�������ɽ�ϡ�1�ĤΥ˥塼������������������������������ǤϤʤ�������λ��ݤξ�����������ʣ���ġ�n�ĤΡ˥˥塼�������Τ�������������������뿿����ɽ�Ȥ��뤳�Ȥ�Ǥ��롣����ŵ��ɮ�Ժ���
���Τ褦�ʿ�4�ο�����ɽ��3�ο�����ɽ����Ĵ��ܲ�ϩ�����̤��Ȥ߹�碌��ɽ����ľ�����Ȥϲ�ǽ�������� ���ˡ���������Ƥ���AI�����ӥ������Ƥ��륵���Фν��Ѳ�ϩ�ϡ�2���ϤǤ�̵�����⤷��ʤ��������Ū���������Ϥ�NAND��NOR�����̤��Ȥ߹�碌����ϩ���鹽������Ƥ��롣
�����������ʤ��Ȥ⡢�ե��Υ��ޥ�䡢�ޥ����å�&�ԥåĤκ��ϡ��ֿ�ƬǾ��ȯ�ˤϡ���4�Τ褦�����������ܿ���¿����ΨŪ�������Ѥ���Τ���ľ���פȹͤ����Ƥ�����
�Ȥ������Ȥϡ��˥塼���Ԥ��黻���Ϥ�����4�ο�����ɽ��ư���Ԥ�����������ϩ���Ѥ���������AI��ϩ���߷פ˸����ΤǤϤʤ�����¿���Ϥγ�ΨŪ�������Ѥ���ȡ�Ǿ�Τ褦�ˡ���Ū�˾��ʤ��������Ϥ���Ū���������Ԥ���Ȥ������ȤʤΤ���������
����ν��Ѳ�ϩ�ϡ�CMOS���Ѥ��Ѥ��ơ����Ū�����ܿ��ξ��ʤ�AND��NOR�ʤɤ���ܲ�ϩ�Ȥ�����ϩ���Ϥ��Ѥ߾夲���ˡ�������Ȥ����褿���������١�����¿���Ϥγ�ΨŪ������ͭ������ͤ��Ƥߤ�٤��ǤϤʤΤǤϤʤ����������Ȼפ����̤Ȥʤä���
��
1. �ޥ����å�&�ԥåĤΥ�ǥ�Ǥϡ����˥塼����α黻ư����ʥץ����νŤߤ�ɽ���٥��ȥ��� { wi; i=1,2,3,������N }�ȡ����Ͽ��椬ɽ���٥��ȥ��� { xi; i=1,2,3,������N }�������ͤ��褺��ᡢ���������ͤ����͡�b�ˤκ��ˡ��������ؿ� (��) ����Ѥ����ƽ����ͤ����ʻ��ͻ��� 2�ˡ�
y=��() -b
���ߤǤϡ��ؿ� (��) �Ȥ��ơ����ޤΤ褦���͡��ʴؿ������פ����Ƥ��ꡢ���Ӥ˱���������롣
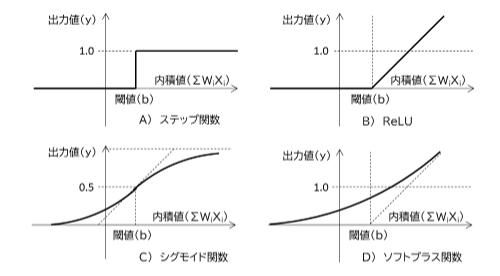
2. �������͡������Ű̡ˤϡ��ֺ�˦���¸�ߤ������ͥ�꤫��ή������ʥȥꥦ�।�����+���̤ȡ�ή�Ф��륫�륷���।�����+���̡�ή��������ǥ������-���̤����礦�Ű̡פȤ�����ΤΡ���̩�ˤϡ��֤����Υ������ή���̤ˤ�äơ��Ṳ̋ε徺���ݤ��������Ψ���Ѥ��פ��ᡢư����졼���ϰϤ�����Ȥ���Ƥ�������ͻ���5�ˡ�
���ͻ���
1. Nilsson, N. J., "Probabilistic Logic" Artificial Intelligence, vol.28, pp. 71-87, 1986
2. Neumann, J. V., "Probabilistic logics and the synthesis of reliable organisms from unreliable components", Automata Studies (ed. by C. E. Shannon and J. McCarthy), Princeton University Press, Princeton, N.J., 1956.
3. McCulloch W. S. & Pitts, W., "A logical calculus of the ideas immanent on nervous activity." Bulletin of mathematical biophysics, vol. 5, pp. 115–133, 1943.
4. McCulloch W. S.; "What is a Number, That a Man May Know it, And a Man, That He May Know a Number?" General Semantics Bulletin, vol. 26/27, pp.7–18, 1960.
5. Web���Ǿ�ʳؼ�ŵ (2012ǯ4��3����)�Ρ����͡פι�
6. ������Ƿ������Ǿ����ǽ��ʪ�����ס�ʪ�����桦�Ż��ǡ�Vol.8, No.1, 2020ǯ2���




