人工知能への道(3);「対話する構造」の重要性
人工知能の父と呼ばれるマービン・ミンスキー氏は、1961年の論文(参考資料1)の中で、「知性(Intelligence)は、外部情報との関係が強い脳内の世界モデルとマインドとの間の内省(Introspection)によって発現する」という複数の計算機構(マルチエージェント)間の対話モデルにて、人間の知的活動を説明しようとしていた(参考資料2)。 今回は、「複数の計算機構間の対話」が計算能力をステップアップさせる鍵となる方向でもあると数学的に証明されていることを紹介する。
“Computing”の源流
”Computing(コンピューティング)”という英単語は、「計算」に置き換えるのは一般的だが、「計算」を英訳すると、なかなか“Computing”や“Computation“は思い浮かばない。 ”Computing”と「計算」に共通項があることがわかるのだが、共通しない部分は一体何なのか?筆者は、ずっとその意味することが気になっていた。 しかし、ある時、中世イタリアのガリレオ・ガリレイ(1564-1642年)の言葉を眼にした時、探していた”Computing”のルーツに出合ったような気がした(注1)。 それは、「宇宙は数学の言葉で書かれている」であった。
“Computing”とは、数学の言葉(論理と計算)による表現を言っているのではないか?“Computing”を狭く理解すると、四則演算や電卓を使った計算になりかねない。しかし、数学者が興味する所は、宇宙に起こりうる全現象であり、この世の真実である。 ガリレオと数学者は、「真実の姿は数学を通してしか理解できない」と言っていると筆者は理解した。
“Computing”は特定の人間の信条や感性に基づく演算や論理ではない。 信条や感性に基づく演算や論理は、個人個人で異なり得る。しかし、計算で表現できる論理は、生物としての人間の能力の限界を超越し、この宇宙の中で共有可能で最も信頼できる世界観を提供しうる。数学者はそのように考えたのではないだろうか?
ガリレオに次いで、人間の能力の突破を狙い、共有可能で信頼できる世界観を提供する作業を提唱した人物は、19世紀のドイツの数学者ゴットロープ・フレーゲ(1848-1925年)とデビット・ヒルベルト(1862-1943年)であると思う。 彼らは、「人間が信条や感性を通じて経験する世界観や論理は、本物ではない可能性がある」と見做していたと筆者は思う。 彼らは、「直感を排し、皆が真実であると見做す公理に基づいて矛盾の無い知識の体系を構築しよう」という活動のリーダであった。 いわゆる「厳密学」の構築活動である(注2)。 「厳密学」は、人間の経験的な理解を排除し、信じるに足る仮説(公理)を出発点に、数学と論理学によって客観的に世界の姿を理解しようとする。 それは、人間の理解は、個人の経験に制約されてしまう主観となりがちだからである。
ヒルベルトは、1900年のパリ万博と共に開催された国際数学会議に、「ヒルベルト・プログラム」を提示したという(参考資料3)。ヒルベルト・プログラムの趣旨を筆者なりに意訳すると以下の表現となる。
(1) 既存の知識を、さまざまな人によって再利用できる形式(定理)に表現し直し、再検証し、人類の共有知識として受理を進める。
(その新しい表現には、矛盾やパラドックスが無いと第三者に検証されることを求める。その目的は、知識を個人の所有から独立させ、複数の人間の参加の元で拡大させるためである)
(2) 未だ仮説としか呼べない段階の知識に対しては、命題としての証明作業を進め、更に、第三者検証することによって、人類の共有知識として受理(もしくは拒否)するかどうかを判定する。
ヒルベルト・プログラムは、オープンイノベーションの方法論であり、研究者や開発者が持つべき会話マナーでありルールであった。 そして、その方法論、マナー、ルールが、20世紀後半の集積回路技術やIT技術構築を進めたと、筆者は見る。 巨大開発を必要とする集積回路産業は、フレーゲとヒルベルトが提唱した方法論、マナー、ルールなしには成り立たない産業である(注3)。
さまざまなユースケースにて再利用可能な知識は、「汎用性」がある時に価値が高く、そして重要である。
一方、矛盾やパラドックスが存在すると、既存の定理と組み合わせて論理を合成することができないため、価値が低く、受理するレベルにはない。 汎用性がないことは、危険であり信頼性が低いということでもある。
信頼するに足る命題(言語)の表現は厳密でなくてはいけない。 無限大(Infinity)や特異点(Singularity)も警戒された。 それらはパラドックスの原因となりうるからである。「無限大」や「無限小」を表現する数学記号は存在するが、共に実在するかどうかは証明されてはいない。
ヒルベルト・プログラムが進めた学術文化によって、知識が人から独立し、多くの人々の頭脳に引き継がれ、深化し拡大していった。 人間の知識が、決して訪ねて行くことができない宇宙の開闢(かいびゃく)の瞬間や、ブラックホールの中や、地球や太陽の中心部の構造にまで及んでいるのは驚異としか言いようがない。
AIコンピュータは「思う」のだろうか?
今も、ほとんどの人は、AIコンピュータが本物の知性持つようになるとは考えていないと思う。しかし、ヒルベルトが「知識の形式化要請」を行う際には、「数学的知識は機械的に構築可能である」との洞察があったのではないだろうか? 少なくとも、アラン・チューリングは、1948年以降、機械が知性を獲得する方法は議論し得るとの趣旨を複数の論文にて発表していた(参考資料4―6)。
1928年、ヒルベルトは、特に「決定問題」への注目を呼び掛ける(参考資料3)。「決定問題」とは、「受理」もしくは「拒否」を判定するタイプの問題である。
1936年、その「決定問題の解決に向けて方法論」として、アラン・チューリング(1912-1954年)は、チューリングマシンと呼ばれることになる仮想コンピュータを発明し、その構造と機能を提示した(参考資料7)。「決定問題」への解決に向けてチューリングがとった戦略を筆者なりに意訳すると、以下となる。
(1) 「命題を解く作業」を「論理と計算の手順」とみなし、その概念を「アルゴリズム」と表現した。
但し、この「アルゴリズム」は、学習やトレーニングの過程は含まない。
(2) 「アルゴリズム」を処理するチューリングマシンの内部構造(アーキテクチャ)を具体的に提示した。
現代のコンピュータの基本構造が、この時、実質的に発明された。
(3) 「命題が受理可能かどうかか」は、「チューリングマシンの動作が『効果的に計算できる時間』で停止(動作完了)するアルゴリズムが存在するかどうか」と同じであることを示した。
つまり、「決定問題」を「チューリングマシン(仮想コンピュータ)の停止問題」という表現に置き換えた。しかし、アルゴリズムが見つかったとしても、現実的な時間内に動作が完了しえないのであれば、証明が完了するのかどうかを知ることはできないので、証明したことにはならないということである。
チューリングマシンが現実的な時間内に動作が完了するかは、チューリングマシンのアーキテクチャが関係して来る。 「現実的な時間内に動作が完了するか」と「チューリングマシンのアーキテクチャ」の関係は、その後、「計算複雑性理論」(もしくは、「計算量理論」)の世界を切り開き体系化され、「計算可能性問題」とも呼ばれるようになった。
「計算可能性問題」は、筆者の理解した、以下の二つの作業が生ずる問題である。
(A) アルゴリズムを、現実的な時間内に動作完了するに必要な「動作ステップ数や必要なメモリ容量」の観点(計算量)にてランク分けする。
(B) 複雑なアルゴリズムの計算に対して効果的なアーキテクチャを持つよう、チューリングマシンのアーキテクチャ拡張を定性的に考え、その新しいアーキテクチャのクラスの有効性を計算量のランクとの関係で見積もる。
計算量のランクの定義
アルゴリズムが動作完了するまでの計算量のランクとしては、「アルゴリズムが完了するまでのステップ数や必要なメモリ容量」をパラメータ(n)として、例えば、
・ Polynomial Time (P) : nの多項式で表せる計算量
・ Exponential Time(EXP) : nの指数関数で表せる計算量
・ Doubly-Exponential Time (NEEXP): nの「二重の指数関数」で表せる計算量
が定義されている(後述する表1の左側の欄の表現)。
古くは、「計算量がPolynomial Time(P)に収まることが、現実的な時間内に動作が完了することである」とされて来た。
チューリングマシンのアーキテクチャ議論
チューリングマシンのアーキテクチャに関しては、以下のような拡張が検討され、それぞれが新たな仮想コンピュータのタイプとして定義されて来た。 代表的な例は、表1に示すように(各略語は表1参照)、
(1) DTM:古典的チューリングマシン
(2) メモリ容量を巨大化するバリエーション
(3) NTM:ステートマシン回路を大量に搭載して、分岐後の処理のいずれかで動作完了した場合には、マシン全体が「動作完了」とする
(4) NPTM:乱数発生器を搭載して、ランダムにパラメータを変更しながら、処理を複数回進めることで、「受理」や「拒否」が出るパターンを調べ、統計的に証明を進める
(NPTMを有効に機能させるには、下の(5)の「対話構造」が必要と筆者は思う)
(5) IP:2台の計算機構(エージェント)間が対話することで、(4)の統計的証明を進める
(6) AM:2台の計算機構(エージェント)間の一方を非常に高度な知識と能力を持つ「証明者」、他方を「検証者」とし、両者が対話することで(5)の統計的証明を進める
(7) MIP:対話型証明システムで、非常に高度な知識と能力を持つ「証明者」を複数台用いる
(8) MIP star:複数の量子コンピュータ間で量子もつれ現象で互いに干渉する「複数証明者」を持つ対話型証明システム(通常、MIP starは「MIP*」と表記される。)
等々である。これらのチューリングマシンのタイプは、表1の右側の欄に記載した。

表1 アルゴリズムの複雑さ(もしくは計算複雑性)を計算量という概念でランク分け 欄の右側は、そのランクを定義する際に引用される仮想コンピュータのタイプである。 出典:参考資料3-10を参考に筆者が作成した
アルゴリズムが現実的な時間内に動作完了するに必要な「動作ステップ数や必要なメモリ容量」は、チューリングマシンのアーキテクチャを行うと関わりがあり得るため、この辺の議論や用語の定義は、正直言って非常にわかりづらい。しかしながら、チューリングマシンのアーキテクチャの議論は、汎用コンピュータのロードマップとも見ることができる内容であるため、集積回路に興味を持つ身としては、これらは決して見逃すことのできない議論である。
Human IntelligenceもAIも、MIP star未満
改めて、表1を見て頂きたい。 集積回路の観点から「チューリングマシンのタイプ」をみると、これは、計算効率を向上させるためのマシンの改良議論であった。
「MIP star」は、量子力学をフルにシミュレーションできる装置を意味する。 計算リソースが十分に大きければ、理屈の上では、宇宙の現象を再現可能である。 従って、当然ながら人間の脳も人工頭脳もシミュレーション(もしくは、エミュレーション)可能である。 つまり、Human Intelligence(HI)もArtificial Intelligence(AI)も、その計算量は、「MIP star」未満である。また恐らく、HIもAIも、古典コンピュータのモデルであるDTMやNTMよりは、高度な能力を持つ。
NPTMは、IPやAMの「対話構造」を機能させる計算機構であったことを思い出していただくと、HIを位置付け可能な場所は意外と少ない。ズバリ言って、IP(AM)、もしくは、MIPと言うべきであろう。
それらの特徴は、以下のように二つある;
・ Random化(確率的動作を導入する機構)の追加
・ 対話型機構(複数の計算機構による、高度な知識と能力を持つ「証明者」と「検証者」の役割分担)
IP(AM)の構造を図にしてみると、図1のようになる。この構造は、冒頭に引用したマービン・ミンスキー氏の1961年の論文(参考資料1)の中で示した「知性(Intelligence)は、外部情報との関係が強い脳内の世界モデルとマインドとの間の内省(Introspection)によって発現する」という複数の計算機構を想定した対話モデル(参考資料2)と酷似する。同じだと言って良いのではないだろうか?IP(AM)の構造は、AI(特に、強いAIやAGI(汎用AI))を構成する時に、最も注目されるべき構造だろう。
次回、マービン・ミンスキー氏の指摘に立ち戻り、その比較を継続してみる予定である。但し、この図1では、学習やトレーニングの過程は未だ含まれていないことには注意が必要である。
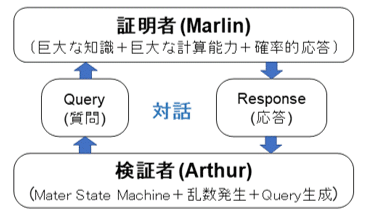
図1 Arthur-Maline型のInteractive Proof Systemの想定構成図 MIPの場合には、証明者(Marlin)が複数実装され、検証者(Arthur)は、それら複数の証明者と対話し、その対話によって、証明すべき範囲を狭めてゆく。 出典:参考資料8-13を参考に筆者が作成
注
1. 米国のリチャード・ファインマン(1918-1988)や英国のデビッド・ドイッチェ(1953-現在)も同様の主張を行っていたことを、筆者は最近知った。 参考資料8-9によると、両者の表現は、「自然界の事象を扱うコンピュータは量子力学的現象を利用して動作する必要がある」であった。 量子力学の発見やコンピュータの発明以降であるため表現は異なるが、「量子力学=宇宙」であり、「コンピュータの動作=数学の言葉」と見るべきであり、そのように見ると同じ趣旨となる。
2. フレーゲは、公理に基づいて矛盾のない論理の体系を構築しようとした。 彼の思想を広めたのは、ジュゼッペ・ペアノ、バートランド・ラッセル、ルートヴィヒ・ウィトゲンシュタイン、エトムント・フッサールらの哲学者であったと言われている(参考資料5)が、その精神を20世紀の科学とIT産業の勃興に結び付けたのは、デビット・ヒルベルトであった。
3. 「日系企業は、一般にロジック半導体の事業に弱い」と筆者は思うが、その弱さは、ヒルベルトが求めたような知識を拡大させる方法論や、会話マナー、ルール、仕様表現の厳密さ、オープンイノベーション戦略の弱さと関係があるのではないかと思う。
参考資料
1. Marvin Minsky, M., “Steps toward Artificial Intelligence”, Proceedings of the IRE Contents, Vol. 49, 1961.
2. 岡島義憲、「人工知能への道(2):Intelligenceとは何か」、セミコンポータル (2021/07/28)
3. ウィキペディアの「ヒルベルト・プログラム」、2021年6月27日版。
4. Turing, A.M., “Intelligent machinery (1948), A Heretical Theory”, Philosophia Mathematica, Vol. 4, Issue: 3, 1996.
5. Turing, A.M., “Computing machinery and Intelligence”, Mind 59: pp 433-460, 1950.
6. Turing, A.M., “Can a Machine Think”, The World of Mathematics, edited by James R. Newman, vol. 4, pp. 2099-2123, Simon & Schuster, 1956.
7. Turing, A.M., "On Computable Numbers, with an Application to the Entscheidungsproblem"、1936年5月28日提出。
8. 丸山不二夫、「コンピュータ・サイエンスの現在―MIP*=RE定理とは何か?(2):計算可能性理論と計算複雑性理論」
9. 丸山不二夫、「エピソード 3:情報過程は物質過程である--Church-Turing-Deutsch Principle」、Web-Content ;
10. Goldwasser, S., Micah, S., and Rackoff, C., “Knowledge Complexity of interactive proof systems”, Proceedings of the 17th ACM Symposium on theory of Computing, 1985.
11. Babai, L., “Trading Group Theory for Randomness”, Proceedings of the17th ACM Symposium on Theory of Computing, 1985.
12. Babai, L., Moran, S., "Arthur-Merlin games: a randomized proof system, and a hierarchy of complexity class", Journal of Computer and System Science, 36 (2): 254–276, 1988.
13. Ben-Or, M., Goldwasser, S., Kilian, J., and Wigderson, A., “Multi prover interactive proofs: How to remove intractability assumptions”, Proceedings of the 20th ACM Symposium on Theory of Computing, p.113-121. 1988.



