ニューロチップ概説 〜いよいよ半導体の出番(5-1)
このシリーズ最後の第5章は、動向を今後について述べている。特に、IBMが開発したTrueNorthニューロモルフィックチップについて、特にディープラーニングという観点から見た回路構成や特長などについて解説している。(セミコンポータル編集室)
著者:元半導体理工学研究センター(STARC)/元東芝 百瀬 啓
第5章: ニューロチップ〜本戦に突入:動向と今後
最後の章となる第5章では「動向と今後」と題して、最初に発表された2014年8月から既に2年を越える時が経っているが、最近の新しい報告もあり新しい顔を持ったニューロモルフィックチップであるIBMのTrueNorthを採り上げる。第3章でも述べたが、本寄稿ではTrueNorthの構成・動作を概説するが、ニューロモルフィックチップとして期待される人間の脳により近い科学的な側面よりも、現在のディープラーニングのもたらすある意味単純な性能の側面より比較説明を行う。新しい顔を持ったTrueNorthを圧縮という切り口からの解説も試みる。中盤の5.2節では本寄稿の技術の最後の説明として、ネットモデルの効率化と圧縮技術の合体により、もたらされる一定レベルの究極の姿に迫る。そして最後に5.3節で今後の課題を概説する。
5.1 ニューロモルフィックチップ〜回路構成とディープラーニングから見た位置付け
5.2 究極の姿へ(一定のレベルへ)〜シンプルなモデルへの適用とNMTへの展開〜
5.3 最後に〜今後の動向と課題〜
5.1 ニューロモルフィックチップ〜回路構成とディープラーニングの視点からの位置付け
本節ではニューロモルフィックチップとして、IBMがDARPAのSynapseプロジェクトの一環として研究・開発し、2014年8月に雑誌Scienceで発表したTrueNorthを取り上げる(参考資料84、85)。その構成を説明するとともにディープラーニングという極めて工学的な観点からこのチップを見てみる。そのため、逆にニューロモルフィック的な要素に関しては極力簡潔に述べる。
(1)概要・・・人間の脳実現を目指して
Synapseプロジェクトの最終目標は、人間の脳の実現である(2020年以降か?)。神経細胞に相当するニューロンとシナプス(メモリ)からなるコア(256ニューロンを内蔵)を64×64のアレイ状に配置し、合計4096コアを集積したTrueNorthチップ(17mm×25mm)が図43の左下に示すように構成される(参考資料84)。2014年に発表されたチップだ。2014年から2015年に掛けて、NS1eボードをIBMは公開し始めた。一つのTrueNorthチップが載っている。そもそも、TrueNorthのアーキテクチャは、コアからのパケット通信を基本としていることから、理想的にはシームレスにコア拡張、チップ拡張が可能で当然ボード拡張も容易だ。2015年夏には、図の右下に示すように48ボードを連ねた48×のシステムを公開している(参考資料105、106を参照)。骨格だけだと、図の右上の挿入図に示すように、人間の脳に対して1/1000のポジションまで来ている。それ以降最近(2017年前半)まで規模拡大の情報はない。
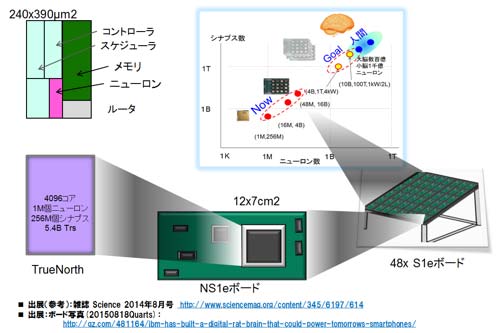
図43 TrueNorthのコア、チップ、ボード構成と、プロジェクトの目標トレンド
参考資料84、85を参考に作成、ボード情報は参考資料105、106.
図44にTrueNorthの概要一覧を示した。図43のニューロン回路(赤色部)を時分割多重で使いまわす、いわゆる仮想ニューロン方式である。1つのニューロン回路を1msecに256回使い回す。またクロスバー方式を用いているが、同じく仮想クロスバー方式でもある。仮想であることを除くと、まさしくSRAM(メモリアレイと積和演算部は最近接に配置されていないが)である。入力(ロー)側は256個の軸索(アクソン:Axon)、出力(カラム)側は256個のニューロンが並ぶ。クロスのポイントが256×256となりシナプス接続を形成する。カラム方向に積和の処理を行う。実際には積和の作業は1ロー毎に行われる。コントロール回路でアクソンへの入力値(0, 1)とシナプス接続情報(0,1)の積をとり、情報(1のみ)をニューロン回路に投げる。この作業をカラム方向にシーケンシャルに繰り返し行う。
一方、ニューロン回路ではコントロール回路からの情報(1)を受け、その都度、ロー番地(アクソン)、カラム(ニューロン)番地で決まるシナプス負荷を元にニューロンモデルに従い演算し条件が整えばスパイク出力を出す。出力はスパイクとしてチップ上のコア、もしくは他のチップのコアへルータを介してパケットとして伝播される。なお、学習の機能は搭載されていない。実行だけのチップである。

図44 TrueNorthの概要仕様 (参考資料84、85を参考に作成)
転載元:STARCでの調査報告書より転載.
各種のネットワークモデルとハード(TrueNorth)とのインターフェースはコアレットというプログラム環境により接続される。応用例として多物体検知・認識で73mW、800GOPS/Wの性能の報告があった。低消費電力であることからエッジ応用を当初より狙っている。特に2015年夏より米国にて” Brain-inspired Computing Boot Camp”,なるものを主催(参考資料107)、多くの米国の大学を中心に数十の研究機関が参加、エッジ系をターゲットとしたアプリケーションへの実用化の活動を継続しており、最近その成果を発表した(一部/参考資料108)。このキャンプは残念ながら国防省が関連しており、日本からの参加は難しいようだ
(2)回路構成
重複する点もあるが、回路構成に関して図45を用いて簡単に説明する。参考資料85を参考に作成している。かなり複雑だ。入力側に256個の入力(軸索:アクソン)の端子があり、かつ16ステップ(1msごと、16msまで)の時間を調整できる16×256ビットのメモリマトリクスをおかれている。ダイナミックに時間調整をするものではなく、事前のオフラインで行った学習の結果に従ったスタティックなネットワークモデルを構成するためのものである(現時点での筆者の理解)。内部は非同期ではあるが、グローバルクロック(1ms周期)により同期させるためのタイミング調整用でもある。
クロスバーのクロスポイントは、バイナリービット(0、1)からなる接続情報のみを有するシナプス接続である。それに加えて、入力ロー側のアクソンと出力側のニューロンで決まるシナプス係数と称する重みを持っている。4種類の9ビット(-256〜255)の重みだ。種類はアクソンにより決まり、9ビットの値はニューロンにより決まる仕組みだ。興奮性(プラス)とか抑制性(マイナス)といったタイプはアクソン側で決めて、その重み(大きさ)はとなるとニューロン側で決まるということだ。コードブックが用意されている。学習の段階でこの表は決定されSRAMに格納される。その点から、TrueNorthはバイナリーと言われているが必ずしもそうではない。また後で述べるが、コードブックを使用する点は前節4.3節で述べた量子化の一つであるクラスタリングと同じだ。
カラム方向にロー毎に逐次計算される結果がニューロン回路に入り、その都度和の処理が行われる。ポテンシャルが変化する。結果、単純には事前に決められているしきい値より大きくなればスパイクが出力され、逆に小さければスパイクは発生しない。スパイク発生後もしくはグローバルタイミング1msec毎にゼロにリセットされる。以上がパルス入力から、パルス出力までの手順だ。しきい値を持つ点は前節4.3節のPruningに似ている。貢献度の少ない(重みが小さい)ものは最初から参加も許されない。ダイナミックに処理される点では同じく前節4.3のゼロスキップに近いと考えた方が良いかもしれない。
論文によると一例として100入力に対して1回のパルスが出るようにしきい値制御されるのが標準のようだ。1コア当たり5スパイク/1ms程度とのことだ。出力はかなり疎(Sparse)だ。もちろんその頻度は固定ではない。しきい値を低くすればパルスの頻度は高まり、演算性能は上がるが同時に比例して消費電力も上がる。しきい値を低くすると10倍程度は頻度が上がるようだ。この頻度、すなわちしきい値が低消費電力さらには動作速度の要になっている点がIF (Integrate and Fire)型ニューロンモデルの特徴である。通常のFLOPS(Floating-point Operations Per Second)という性能表記に対して、一回のパルス発生をSynaptic Operationと見なしたSOPS (Synaptic Operations per second)という性能表記を使用している。FLOPSとSOPSの比較は難しい。SOPSの価値も明確にする必要がある。例えば依存性の大きいしきい値が何によって決まるかの定性的もしくは定量的な理解が欲しい。ニューラルネットワークでもPruningなりゼロスキップ、さらには量子化を施した際、実効処理速度という表現を用いることがある。これに近い考え方が理解しやすいと考えている。
出力はスパイクとしてニューロン回路からルータを通して、パケットとして目的の番地に送られる。チップ、コアの番地、そしてアクソンのロー(行)の番地からなるネット接続情報だ。時間情報も付加する。アクソン遅延と称する1msecを単位とするタイミング情報だ。スパイクのコア間の同期をとるためだけに使用されている。パケット情報は、学習時の段階で決められる。スタティックなネットワーク構成を決めるためだ。なお、学習時にはさらにシナプス負荷およびシナプス接続も決める。ネット構成が決まり、重みも決まれば学習でのネットワークモデルは完成する。実行の前にパケット情報と負荷、接続情報はコア内のSRAMにストアされる。
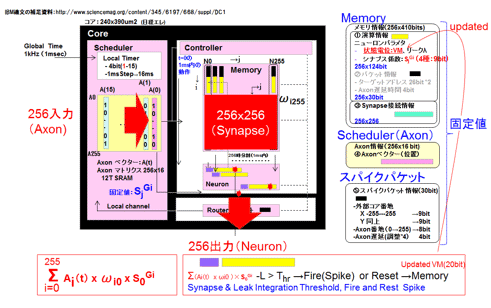
図45 TrueNorthの回路方式: (参考資料85を参考に作成した)
出典元:STARCでの調査報告書より転載
(3)ニューロモルフィック/TrueNorthの特徴と動向〜ディープラーニングとの架け橋
ニューロモルフィックは、バイナリー(TrueNorthでは正確には入出力データのみ)での演算処理に加えてスパイキングでの情報伝播が疎であることから、その低消費電力性が実用的には魅力だ(複数物体検知が70mW)。そうなると、ディープラーニングの手法を実装できないか、とりわけ際だった成果を上げているCNN(正しくは畳込みの技術)をニューロモルフィック上に実装できないかと期待されてきた。今までなかった両者に橋を架ける取組みだ。
実はこのことは、2014年発表当時より議論されている狭義のニューラルネットワークとニューロモルフィックのどちらが優れているかという議論に一定の判断が出る取組みでもある。中々難しいと漏れ聞こえていたが、2015年後半より2016年11月にかけて論文報告(実際は改訂が繰り返され)があり進展が伝えられているので、この項でその技術的な内容を解説する。状況を言うと中々判断が難しい、少し理解するのに時間が掛かるという状況である。
課題は、以下の二つである。
-スパイキングと誤差逆伝播法(バックプロパゲーション法)の微分と相性が良くない(本質)
-クロスバー方式と畳込み層の組み合わせが難しい(実用上の課題)
TrueNorthのプロジェクトのメンバーより2015年末以来2つの提案がなされた。第2章の2.8節で紹介した参考資料43と44(最新版は110、120)である。前者は2015年12月のNIPS(The Conference and Workshop on Neural Information Processing Systems)で発表された。後者は、2016年の3月の初版を皮切りに最終版が同年10月に発表された。2つともCoreletの開発に携わったソフトウェアエンジニアのEsser氏の発表である。全体のシステムに関しては澤田潤氏が論文として発表している(参考資料120)。
(ア) Constrain then train法・・・2つのネットワークでつなぐ!
彼らの2015年NIPSでの提案を解説する。手法に名称がなかったので、便宜上筆者の主張する手法の特徴を使い命名させてもらった(参考資料43)。トポロジーが同じ、2つの学習用(Training network)と実行用(Deployment network)のネットワークを用意する。図46に論文を参考に作成した手法を示した。
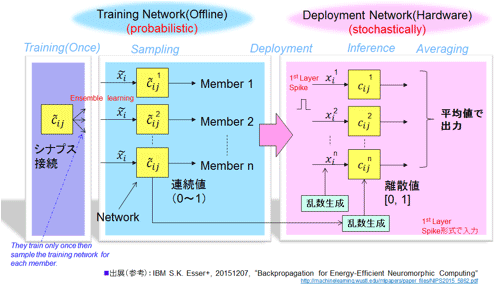
図46 Constrain then train法: 学習時は制約を受け確率的処理、実行は乱数を用いて統計的処理(参考資料43を参考に作成した).
まず学習(図の左側)では、通常のニューラルネットワークの数値に制約(Constrain)を与える。すなわち入出力(xi)およびシナプス負荷値(cij)を0〜1の範囲に変換および限定して取り扱う(彼らはこれを制約と称している)。言うまでもなく連続値なので誤差逆伝播法での学習が可能だ。シナプス負荷情報とバイアス値(図には接続情報のみ)を学習パラメータとして導出できる。それぞれ0〜1の確率値だ。先に、数値に制約を加えることから”Constrain then train法”というようだ。
実行を行うスパイキングネットワーク(右図)において実行処理を確率的(stochastically)に行う。学習で得られたシナプスの接続情報の確率値に従い乱数を発生させ実行する。また性能を上げるために複数の学習モデルを用意し、実行では結果(出力値)を平均する。アンサンブル法と言う。
手法の評価をMNIST(Mixed National Institute of Standards and Technology database ベンチマーク用データベース、手書き数字0、1、・・・9の認識テスト、サイズは28×28ピクセル、グレイ)のデータセットを用いて行っている。その際にTrueNorth内のコアは30個使用し、64並列のアンサンブル法を用いている。1920のコアを使用している。結果、99.42%と高い精度を出している。64並列という度合いの多さに少し驚く。
ニューロモルフィックとディープラーニング(Back propagation)との間に架け橋ができたことを示す工学的な意味での最初(知る限りでは)の成功例である。今後はより大きなネットワークにトライすることが期待される。
(イ) 微分値近似法の導入とCNNへの適応・・・こちらが本命?!
二番目の手法である。今年の3月に同じくEsser氏からAirxivに投稿された論文(参考資料44)の内容である。最近、9月以降、IBMが公式に電子情報(参考資料109、110)として配信している技術と成果である。論文は、全5ページの中に新しい手法、CNNの実装、各種ベンチマークの結果が詰められている。CNNへの適用も十分重要であるが誤差逆伝播法をどのように適用したかが注目される。
新しい手法(微分値近似法)
手法は一言で表現すると、スパイキング出力を微分すると無限大になってしまうので、微分値を先に決め打ちしてしまおうという手法である。仮の名称として「微分値近似法」とした。前項で述べた、「Constrain then train法」との関係は明記されていない(全く別物と思われる)。
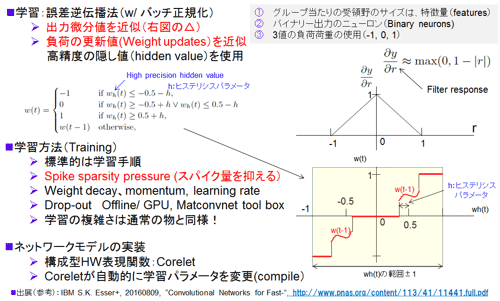
図47 微分値近似法(仮)の内容 (参考資料110、111 最新版を参考に作成)
実際には、他にいくつかの手法が採り入れられており図47に記載した。まとめると学習は、バッチ正規化(Batch Normalization:参考資料31)を使った誤差逆伝播法を用いている。そこに前述の微分値近似法(図47の△近似)、ヒステリシス(一時間前の情報を一部使う)を用いた隠れ重みのw(t)アップデート手法、さらにSpike sparsity pressure(これは学習実行時の工夫)なる手法を用いている。微分値近似法は挿入図に示すように、変数r(フィルタレスポンス値)の変動に対して三角状の微分値を決め打ちしている。学習の部分に関して当初は十分に公開されていなかったが正式論文となり参考資料111(10月11日)にかなり細かい手順が記されている。
CNN実装でのポイント
a.重みは3値(Trinary -1, 0, 1): 2014年当初より大幅に簡素化(抽象化)している。ポイントはシナプス値(重み)が図47の右下グラフのように3値(-1, 0, 1)を取る点だ。±1は興奮性と抑制性シナプスに対応する。0を加えているのはより精度を上げるためと想定される。この3値を取れる様にするために、(1)アクソンのタイプを2種類(前述では4種)としその値はプラス1とマイナス1(固定:前述では9bit)、さらに(2)TrueNorthの実装ではペアー入力方式をとる。一つのスパイク信号をプラス1とマイナス1の2つのアクソンに同時に入れる。そして、両信号を(3)シナプスマトリクスのカラム上で和を取りプラス1(プラス側だけオン)、マイナス1、そしてゼロを作る(両方ともシナプス接続をオンさせる)。結果ロー側の効率さらにはチップの面積効率を1/2と犠牲にして3値シナプスを作り出している。ちなみに、アクソンへは1入力としシナプス負荷を3種類とすることも可能と思われる。なぜペアー入力としたのかは不明。なお、ほぼ同時進行でニューラルネットワークでも多くの研究、特にモントリオール大学のBengio先生のグループを中心にBinaryおよびTernary(上記のTrinaryと同じ)の研究がなされてきた。独立に進んだとはいえ時期的には同期している。
b.畳込み層の実装: ペアー入力であることから入力の数の最大は128となる。ネットワークの配置方法の考え方の基本は、畳込み層のフィルタは4次元(入力特徴マップ数、2次元フィルタ、出力特徴マップ数)だが、不可分の最初の3次元分を1つのカラムに対応させる点にある。その結果、1サイクル(1ms)で3次元の積和が一つのカラム、ニューロンで行える。(なお、幾つかの別案も可能である)。
図48に畳込み層の展開を図示した。4次元目の出力特徴マップへの対応はカラムの横方向展開で対応する。出力特徴マップの最大数は256マップとなる。一瞬(1ms)で計算が終了する。ただし、1コアで処理出来るのは出力マップの1ノード分だけである。理想的には4096コア存在するので、4096ノード同時処理が可能だ。
しかし、実装上は2つの課題が存在する。(1)フィルターサイズなり入力特徴マップ数が多いとすぐ満杯(128入力)になる。これはクロスバー方式、さらにはニューロモルフィックでは頭の痛い点である。特に後者の場合は途中にニューロン回路を介する。そのことから3次元分のフィルタの積和が一般的には不可分になる。この点への配慮が必要だ。著者らはグループ化という考えを使用している。複数の入力特徴マップをグルーピングして部分和を行う。特徴マップのレベルでいうならば、全結合ではなく部分結合を行う事に相当する。このことは実際のクラス化での全結合でも同様だ。精度を上げようとした際に影響が出る可能性がある。(2)次はTrueNorthのアーキテクチャ特有の入力側での問題で本質的ではない。入力値の複数コアへのマルチキャスティングがやりにくい点だ。対応としてTrueNorthではコアをマルチキャスティング用回路専用として使用する。コア層数のかなりの割合で使用される。
CNN、HGMM(hierarchical Gaussian mixture model)、およびBLSTM (bidirectional long short-term memory)へ適用したベンチマークの結果が出されており、良い結果とのことである。今後より大きな規模のモデルへの適用が期待される。
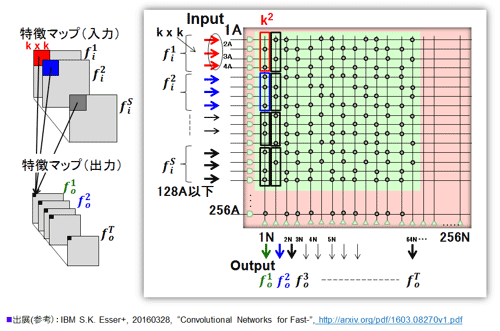
図48 畳込み層のコア(クロスバー)への展開方法:(参考資料45を参考に作成)
(ウ) 圧縮法 (Deep Compression等)と比較 ・・・ かなり強引だが!
図49に標準的なTrueNorthで説明されているパラメータの設定方法を示した。シナプス係数は入力左側の番地(i)と出力下側の番地(j)で決まる方式だ。入力側のアクソンは4種類のタイプがある。そのタイプにシナプス値を割り当てる。
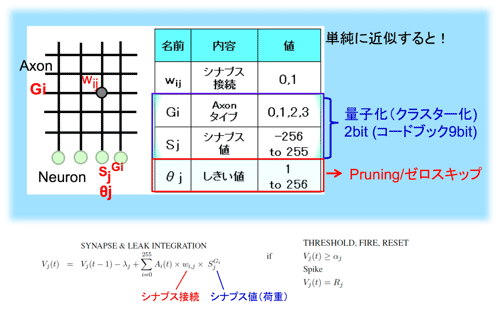
図49 TrueNorthの演算部分を圧縮という視点での近似
量子化:ここで、Deep Compressionの量子化と比較してみる。共にコードブックを利用したクラスター化の手法を用いている。TrueNorthの場合には4種類、Deep Compressionの場合は、一例として畳込み層に256(8ビット)種類、全結合層に32(5ビット)種類を割り当てている。TrueNorthは2ビット、Deep Compressionは平均で5.4ビットだ。またそれぞれの種類は代表値(Centroid)と称してTrueNorthは9ビット(-256〜255)、Deep Compressionは32ビットの値が与えられる。なお、TrueNorthの場合はカラム(ニューロン)の位置により独立して値を256種類選べるが、実はロー(アクソン)側の256ローで共有することから相殺される。結果、比較すると5.4ビット(Deep Compression)と2ビット(TrueNorth)の差とみることができる。
Pruning/ゼロスキップ:同様に、Pruningとスパイキングを考えて見る。共にしきい値により大きなデータ量の圧縮を行っている。前者は接続(重みの大きさで判定)そのもの、後者は出力そのもの(積和の値で判定)を切り捨てる。しきい値は事前に決定される。そして前者はスタティックに、後者はダイナミックに切り捨てが行われる。微妙に異なるが、かなり類似点はある。またDeep Compression等にはゼロスキップといったテクニックもある。ダイナミックに判定している点ではこちらの方が似ていると言える。大雑把にまとめるとニューラルネットワークでは主に使われる活性化関数ReLU(Rectified linear Unit)により、またスパイキングニューラルネットワークは、スパイキングによりデータの疎らさが加速される。
まとめ:通常のニューラルネットワークも圧縮技術を加えることにより、かなりスパイキングニューラルネットワークに近くなってきたとみることができる(実は90年代に両者が比較された痕跡がある)。本寄稿では取り扱わなかったBinary ConnectなりBinarized NetworkさらにはTernary Networkでより近い物になると考える。
そろそろ工学的な意味での検討も一定の段階に入ったと認識している。ニューロモルフィックもしくはスパイキングニューラルネットワークでの新たなステージが期待される。
編集注)百瀬氏の現在の肩書は、北海道大学 大学院情報科学研究科 学術研究員である。




 インサイダーズ
インサイダーズ インサイダーズ
インサイダーズ インサイダーズ
インサイダーズ インサイダーズ
インサイダーズ インサイダーズ
インサイダーズ セミコンポータル編集長
セミコンポータル編集長 半導体関連市場の動向
半導体関連市場の動向 技術コンテンツ
技術コンテンツ 経営・戦略ビジョン
経営・戦略ビジョン トピックス解析コラム
トピックス解析コラム