ニューロチップ概説 〜いよいよ半導体の出番(3-2)
第3章3.2では、ニューロチップで重要な2次元の入力データと、学習の重みに相当するフィルタを積和演算で、スキャンしていく基本演算について述べている。積和演算を基本とするためGPUやCPU、DSPなどで演算できる。(セミコンポータル編集室)
著者: 元半導体理工学研究センター(STARC)/元東芝 百瀬 啓
3.2 回路構成の基本(畳込み層)
回路の説明に入る前に、予備説明を行う。
呼称:チップにより入出力やパラメータの呼称が異なるので、図17の表にまとめた。入力は、入力特徴マップ(通常2次元)と呼ばれることが多い。ノードという場合もある。入力の要素数に関しては入力次元数、ノード数と呼ぶ場合もある。特にいろいろあるのが、パラメータの部分。使用する技術者の分野により異なる。ソフト系のエンジニアはパラメータが主流である。ニューロモルフィック系の技術者は図17の神経細胞の呼称に従って付けている。信号線路の末端(軸索末端)をAxon(軸索)と呼び、Synapse(シナプス)を介してNeuron(ニューロン)細胞に繋がると表現する。
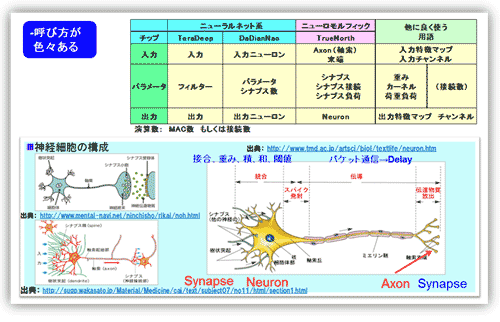
図17 チップの入力、出力、そしてパラメータの呼称と神経細胞の呼称
出典元:STARCの調査報告書より転載
基本回路: 全結合層は積和の単純計算であることから説明は割愛(4.2節で実際のチップで扱う)し、少し複雑な畳込み層の計算に関し説明を行う。畳込み層の計算は以下の3ステップの並列処理(内部計算をし、前側の入力マップ処理をし、後ろ側の出力マップ処理をするイメージ)からなる。「並列処理の手順」と「並列処理の回路」に分けて説明する。
(1) 並列処理の手順
(ア) 並列処理1・・・図18のフィルタ演算処理(積和演算処理)
入力データ(2次元:入力特徴マップ)とフィルタ(重みを2次元化したもの、Kernelとも呼ぶ)との内積を取り、出力(出力特徴マップの1ユニット)する。図の左に示すように横(縦)に1ステップ分スライドして、再度内積を取り出力し先程のユニットの横に1ユニット加える。この作業を入力マップ面内でスライドしながら繰り返す。スライド値はあらかじめ指定される。最近は1が多いが、2以上だと出力のマップサイズは1/4以下になる(Maxpoolingと機能が重なる)。ステップごと(すなわち出力のユニットごと)同じフィルタを用いる。出力マップで見ると全てのユニットに同じフィルタが使われる。フィルタと局所的な内積を取ることと、フィルタの使い回しが畳込み処理の特徴である。そしていかにフィルタ値を使いこなす(リユース:Reuse)かに回路構成の工夫がある。古典的な方法(後述)と、ShiDianNao方式(参考資料81)なりEyeriss方式(列固定データフロー方式(Row Stationary dataflow):参考資料48)がある(4.1節で説明する)。
(イ) 並列処理2・・・図18の入力特徴マップ間処理(加算処理)
入力が図の様にRGBの3入力なら、3回計算して加算しないといけない。その時にフィルタは異なり3種類必要となる。よって、入力マップごとにフィルタと入力値をメモリからロードする必要があり、かつ通常は3入力マップ分計算が終了するまで最終の出力ができない(中間値の発生)。この部分が畳込みの処理計算で一番面倒な部分である。2013年と古いが3D加算回路を専用に持たせ工夫をしているのがTeraDeep社のnn-X(参考資料83)だ。
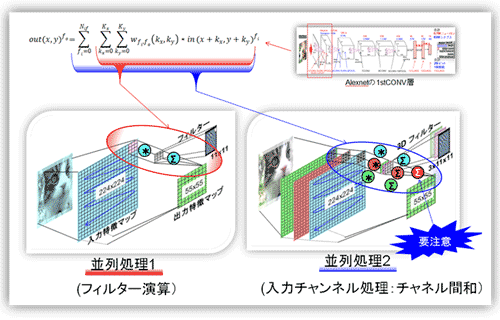
図18 畳込み層・・・並列処理1および2
(ウ) 並列処理3・・・図19の出力特徴マップ計算(独立並列処理)
複数の出力特徴マップを出力マップごとに独立して計算する。そのため比較的簡単である。いわゆる、PE(Processing Engine/Elements)を必要なだけ並べればよい。各チップ共に似たような構成となる。
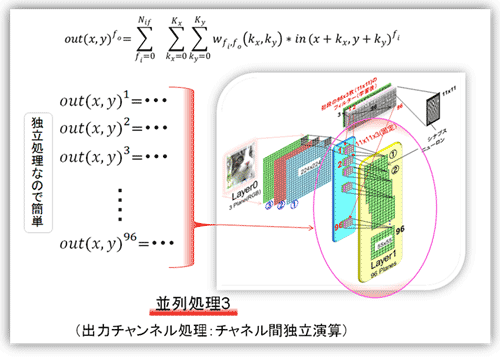
図19 畳込み層・・・並列処理3
冒頭で述べたように、内部計算(積和演算処理)をして、前側の処理(入力マップ間の加算処理)をして、後側の処理(出力マップ間の独立並列処理)をする、3ステップで1層分の畳込み層の計算が終了する。
(2) 並列処理の回路
基本的な回路方式を紹介する。説明および図面は参考資料56(AngelEye)および82を参考にした。まずニューラルネットワークはいくつもの層からなるが、1層ごと逐次行われる。1層の処理のフローを図20で説明する。前層からの出力情報(受け手側から見て入力特徴マップ)を受けて処理はスタートする。通常は、回路の処理規模(総次元数)より入力特徴マップが大きいことからマップを分割(タイル化)して処理を行う(詳細説明は複雑になるので割愛、参考資料56参照)。
データ処理部には、複数のPE(Processing ElementもしくはEngine)コアがPE1、PE2、PE3・・・と置かれ、並列かつ独立に処理が行われる。PEコアの内部には、複数のフィルタ処理(積和処理)を行うConvolver(詳細は次項)ブロック、非線形関数処理ブロック(Non Linear Function:活性化関数とも呼ぶ)、そしてプーリング処理ブロックがシーケンシャルに置かれる。なおPEコア内部で処理が途中の場合には非線形関数処理ブロックとプーリング処理ブロックはスキップして、中間値として戻される。最後に複数のPEコアの出力は、まとめて出力特徴マップとして次層に送られる。なお、PEコアの定義は確定したものではなく、また境界も異なる。本項では比較的オーソドックスで古いタイプを採用して説明した。またConvolverブロックを工夫してプーリング処理、さらには全結合層(FC:Fully Connected層)処理に併用する場合もある。
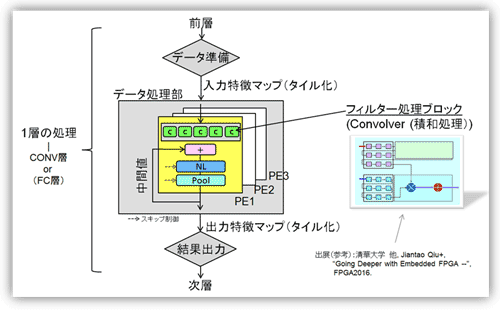
図20: 1層の処理フローの概略図(一例)
(参考資料56、82を参考にまとめた)
(ア) フィルタ演算処理(Convolver回路)
図21にオーソドックスなフィルタ演算回路(Convolver回路)を示した(左側の(a)は参考資料82の図1を、また(b)は参考資料56を参考とした)。(a)の2次元入力特徴マップのフィルタ(3x3)に相当する値を(b)のシフトレジスタに転写する(実際には1画素ごと)。シフトレジスタは3段構成でサイクルごとに1データ分シフトする。1サイクル1ステップごとに、入力データレジスタ(データバッファ)と、同様の3段構成のフィルタレジスタ(重みバッファ)で内積をとる。9並列の積(Multiplier)を行い次段で和をとる。処理の間、フィルタレジスタの値は変わらず、積の相手となる入力データレジスタが変わる。4.1節で扱うCNN用のチップでは基本的に重みは移動しない(Eyerissは、データを追いかけるように重みが横(Row方向)に移動する)。
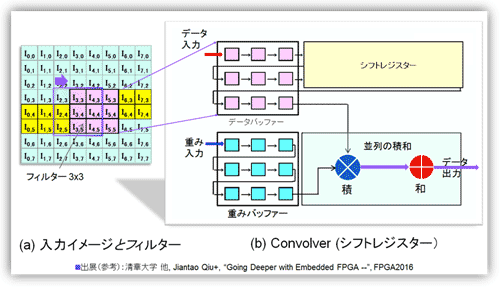
図21 シフトレジスタを用いたフィルタ処理(Convolver回路)
(参考資料56、82を参考にまとめた)
(イ) 3つの並列処理 実例での説明(AngelEyeを参考)
前項で、畳込み層には3つの並列処理があることを図18と19を用いて説明した。ここではその並列処理がどのように回路実装されるか図22を用いて説明する。図はAngelEye(参考資料56)を参考に作成した。例として入力の特徴マップは3枚(猫のイメージでRGBに相当)でフィルタは3x3、出力の特徴マップ数は96枚のケースを用いる。図の左上にフィルタ処理をするConvolverブロック、右側にPEコア、そして左下に全体回路図を示した。
並列処理1は積和演算の並列処理である。3x3のフィルタを使用していることから9並列処理となる。並列処理2はPEコア内部に配列される複数のConvolverブロックにより行われる。入力特徴マップ数が3枚であることから、3個のConvolverブロックが並列処理を実行する。特徴マップ数が3枚と少ないことから並列に処理し単純に加算して次段の非線形処理・プーリング処理に回せる。特徴マップ数が多い場合、例えば200枚あれば、一時中間値として保管して、逐次加算する必要がある。その結果、1枚の出力特徴マップの1ユニットの出力が得られる。フィルタをスライドし(シフトレジスタを1ステップ進める)、処理を繰り返し1枚の出力特徴マップを埋めてゆく。最後の並列処理3は出力特徴マップでの並列処理である。独立していることから単に出力マップ数だけPEコアが並列に並ぶだけでよい。
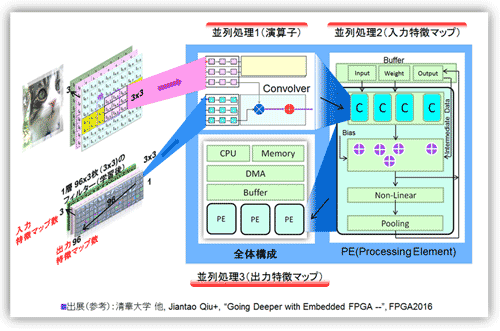
図22 畳込み層処理フローと回路構成、および並列処理の関係
(参考資料56、82を参考にまとめた)
以上がバス方式(次項にて説明)の比較的オーソドックスな畳込み層(CNNネットワークモデルと言ってもよい)の回路構成および処理フローである。なお、非線形処理はALU等の論理回路で、またネットワークの最終層で使用されることが多いSoftMaxは特別な回路は用意せずCPU/MPUで処理される。
(続く)
参考資料は第3章の最後にまとめている。




 インサイダーズ
インサイダーズ インサイダーズ
インサイダーズ インサイダーズ
インサイダーズ インサイダーズ
インサイダーズ インサイダーズ
インサイダーズ セミコンポータル編集長
セミコンポータル編集長 半導体関連市場の動向
半導体関連市場の動向 技術コンテンツ
技術コンテンツ 経営・戦略ビジョン
経営・戦略ビジョン トピックス解析コラム
トピックス解析コラム